线段树是一种基本的高级数据结构,学习它对解决区间问题有很大帮助
这篇文章是我对上学期ACM-ICPC选修课程结课论文的小整理。
1 概述
线段树(Segment tree)又名区间树,是一种高级数据结构,它基于二叉搜索树。线段树经常用于解决区间问题和线段问题,它的优点在于能快速地查询或修改某区间范围的指定标记值。
实现线段树这一数据结构的基本思想:二分法和递归。
线段树基于二叉树形结构,一般采用数组结构储存,树的每个结点包含的信息有:
(1)区间左端点
(2)区间右端点
(3)标记的数据
(4)(可选)懒标记。
一棵表示区间[1,4]的线段树可如图1所示。
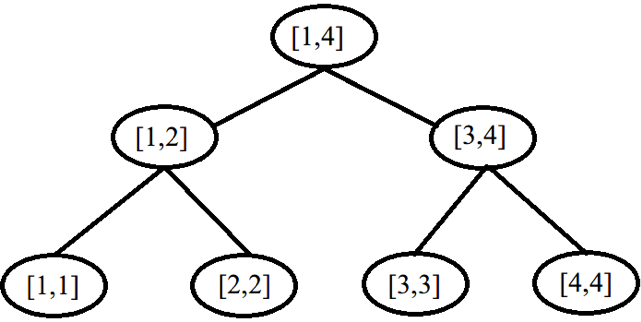
线段树具有以下性质:
性质 1 设结点所表示的区间范围为[left,right],则中点坐标mid = (left + right) ÷ 2,它的左子结点所表示的区间范围为[left,mid],右子结点所表示的区间范围为[mid + 1,right]。
性质 2 若有一结点k,k为其在数组中的位置,其左子结点在数组中的位置为2k,其右子结点在数组中的位置为2k+1。
2 线段树的基本操作
一、引例

分析 可以采用枚举法,对区间里面的每一个数都进行加m操作,算法复杂度为O(n)。但是n的数据范围太大,采用枚举法会超时。可以采用线段树法解决该问题。
二、懒标记
解决上述问题,如果先对区间[s,t]内的所有叶子结点所储存的整数都进行一次加m操作,再对其非叶父结点回溯求和,最后对在区间内的所有数进行求和并查询,其算法的时间复杂度似乎要比O(n)还要高得多。但正如概述里面所说,线段树并不需要对某一区间内的所有叶子结点进行修改和查询的操作。对于引例中的问题,在修改区间数据时,只需要对某一区间所在的结点加上(m×区间长度)即可,该区间的整数和数据就可以直接查询出来了。但是,修改区间和查询区间是可以不同的,在修改区间数据结束后要查询区间数据时,如果要查询的区间是上述修改区间的一个子集,这时就要对上述加法操作下发到子结点,即让子结点也加上(m×区间长度),为实现下发操作,我们要引入一个新的结点信息:懒标记,用于累积区间结点的操作。在查询被修改数据的区间结点的子区间结点数据时,懒标记会发挥其下发累计的加法操作功能。
同样地,如果要修改的区间是某一区间的子集,这时要把结果回溯到父结点,但此时并不需要借助懒标记,因为在某次递归操作结束前可以直接把父结点数据赋值为左右子结点的数据之和。
三、建立线段树
线段树基于二叉搜索树,其数据结构与二叉树形数据结构类似。
本例采用数组来储存线段树的结点,数组长度为4n+1。
#define max_n 1000000
typedef struct _tNode
{
int l;
int r;
int lazy;
int sum;
}Node;
Node node[4 * max_n + 1];
结合性质1和性质2,利用二分法和递归思想,可以很容易地建立一棵线段树。k表示树根的数组下标,l、r分别表示区间的左右端点。
void build(int k,int l,int r)
{
if (l > r)
return;
node[k].l = l;
node[k].r = r;
node[k].lazy = 0;
if (l == r)
{
node[k].sum = 1;
return;
}
int mid = (l + r) / 2;
build(k * 2, l, mid);
build(k * 2 + 1, mid + 1, r);
up(k);
}
up函数执行左右子结点数据之和回溯父结点操作,其代码如下。
void up(int k)
{
node[k].sum = node[k * 2].sum + node[k * 2 + 1].sum;
}
四、线段树区间查询
从根结点开始,判断结点所表示的区间范围是否在所要查询的区间范围以内,如果是则返回结点所表示的区间的和。否则,将懒标记从父结点下发至左右子结点。被查询区间所在的结点可能横跨两个或两个以上的结点,因此在下一步,如果查询区间的左端点小于或等于当前结点区间的中点时,递归结点的左子树,如果查询区间的右端点大于当前结点区间的中点时,递归结点的右子树。最后将得到的左子树的整数和与右子树的整数和相加并返回,即可得到待查区间的和。
int query(int k,int l,int r)
{
int sum_l = 0, sum_r = 0;
if (node[k].l >= l && node[k].r <= r)
return node[k].sum;
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (l <= mid)
sum_l = query(k * 2, l, r);
if (r > mid)
sum_r = query(k * 2 + 1, l, r);
return sum_l + sum_r;
}
父结点下发懒标记到左右子结点时,如果父结点无懒标记记录,则直接返回,如果有,则把其左右子结点的懒标记赋值为父结点的懒标记,再将左右子结点所存储的数赋值为懒标记与左右子结点各自所代表的区间长度之积,最后将父结点的懒标记清空。
void down(int k)
{
if (node[k].lazy)
{
node[k * 2].lazy += node[k].lazy;
node[k * 2 + 1].lazy += node[k].lazy;
node[k * 2].sum += node[k].lazy * (node[k * 2].r – node[k * 2].l + 1);
node[k * 2 + 1].sum += node[k].lazy * (node[k * 2 + 1].r – node[k * 2 + 1].l + 1);
node[k].lazy = 0;
}
}
五、线段树区间修改
与线段树的区间查询类似,从根结点开始,如果当前结点所表示的区间在修改区间内,则将该结点所存的数加上(m×结点区间长度),并且将该结点的懒标记加上m。否则,将该结点的懒标记下发,并且根据区间的跨区情况,递归其左右子树,最后将结点的左右子结点的数上传回溯至该父结点。
void add(int k, int l, int r,int m)
{
if (node[k].l >= l && node[k].r <= r)
{
node[k].sum += (node[k].r – node[k].l + 1) * m;
node[k].lazy += m;
return;
}
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (l <= mid)
add(k * 2, l, r, m);
if (r > mid)
add(k * 2 + 1, l, r, m);
up(k);
}
六、线段树的更多操作
除了区间查询和区间修改外,线段树还可以实现单点查询和单点修改。
int query_s(int k,int x)
{
if (node[k].l == node[k].r)
return node[k].sum;
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (x <= mid)
return query_s(k * 2, x);
else
return query_s(k * 2 + 1, x);
return 0;
}
void add_s(int k,int x,int m)
{
if (node[k].l == node[k].r)
{
node[k].sum += m;
return;
}
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (x <= mid)
add_s(k * 2, x, m);
else
add_s(k * 2 + 1, x, m);
up(k);
}
七、完整代码
#include <stdio.h>
#define max_n 1000000
typedef struct _tNode
{
int l;
int r;
int lazy;
int sum;
}Node;
Node node[4 * max_n + 1];
void up(int k)
{
node[k].sum = node[k * 2].sum + node[k * 2 + 1].sum;
}
void down(int k)
{
if (node[k].lazy)
{
node[k * 2].lazy += node[k].lazy;
node[k * 2 + 1].lazy += node[k].lazy;
node[k * 2].sum += node[k].lazy * (node[k * 2].r – node[k * 2].l + 1);
node[k * 2 + 1].sum += node[k].lazy * (node[k * 2 + 1].r – node[k * 2 + 1].l + 1);
node[k].lazy = 0;
}
}
void build(int k,int l,int r)
{
if (l > r)
return;
node[k].l = l;
node[k].r = r;
node[k].lazy = 0;
if (l == r)
{
node[k].sum = 1;
return;
}
int mid = (l + r) / 2;
build(k * 2, l, mid);
build(k * 2 + 1, mid + 1, r);
up(k);
}
int query_s(int k,int x)
{
if (node[k].l == node[k].r)
return node[k].sum;
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (x <= mid)
return query_s(k * 2, x);
else
return query_s(k * 2 + 1, x);
return 0;
}
void add_s(int k,int x,int m)
{
if (node[k].l == node[k].r)
{
node[k].sum += m;
return;
}
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (x <= mid)
add_s(k * 2, x, m);
else
add_s(k * 2 + 1, x, m);
up(k);
}
int query(int k,int l,int r)
{
int sum_l = 0, sum_r = 0;
if (node[k].l >= l && node[k].r <= r)
return node[k].sum;
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (l <= mid)
sum_l = query(k * 2, l, r);
if (r > mid)
sum_r = query(k * 2 + 1, l, r);
return sum_l + sum_r;
}
void add(int k, int l, int r,int m)
{
if (node[k].l >= l && node[k].r <= r)
{
node[k].sum += (node[k].r – node[k].l + 1) * m;
node[k].lazy += m;
return;
}
down(k);
int mid = (node[k].l + node[k].r) / 2;
if (l <= mid)
add(k * 2, l, r, m);
if (r > mid)
add(k * 2 + 1, l, r, m);
up(k);
}
int main(void)
{
int n, m, l, r, s, t;
build(1, 1, max_n);
printf(“n = “);
scanf(“%d”, &n);
printf(“m = “);
scanf(“%d”, &m);
printf(“l = “);
scanf(“%d”, &l);
printf(“r = “);
scanf(“%d”, &r);
if (l > r)
{
l = l ^ r;
r = l ^ r;
l = l ^ r;
}
add(1, l, r, m);
printf(“s = “);
scanf(“%d”, &s);
printf(“t = “);
scanf(“%d”, &t);
if (s > t)
{
s = s ^ t;
t = s ^ t;
s = s ^ t;
}
printf(“sum = %d\n”, query(1, s, t));
return 0;
}
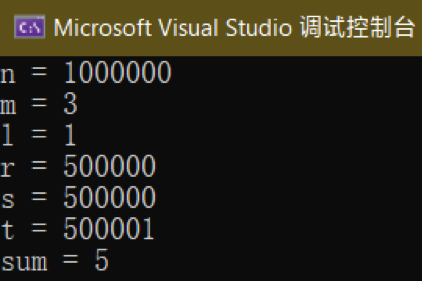
测试结果如图2.7所示。
3 线段树的应用——POJ 2777
链接:http://poj.org/problem?id=2777
Count Color
| Time Limit: 1000MS | Memory Limit: 65536K |
| Total Submissions: 54642 | Accepted: 16407 |
Description
Chosen Problem Solving and Program design as
an optional course, you are required to solve all kinds of problems. Here, we
get a new problem.
There is a very long board with length L centimeter, L is a positive integer,
so we can evenly divide the board into L segments, and they are labeled by 1,
2, … L from left to right, each is 1 centimeter long. Now we have to color
the board – one segment with only one color. We can do following two operations
on the board:
1. “C A B C” Color the board from segment A to segment B with color
C.
2. “P A B” Output the number of different colors painted between
segment A and segment B (including).
In our daily life, we have very few words to describe a color (red, green,
blue, yellow…), so you may assume that the total number of different colors T
is very small. To make it simple, we express the names of colors as color 1,
color 2, … color T. At the beginning, the board was painted in color 1. Now
the rest of problem is left to your.
Input
First line of input contains L (1 <= L <= 100000), T (1 <= T <= 30) and O (1 <= O <= 100000). Here O denotes the number of operations. Following O lines, each contains “C A B C” or “P A B” (here A, B, C are integers, and A may be larger than B) as an operation defined previously.
Output
Ouput results of the output operation in order, each line contains a number.
Sample Input
2 2 4
C 1 1 2
P 1 2
C 2 2 2
P 1 2
Sample Output
2
1
题目大意 有一长度为L cm的板,将板平均分成L块,每一块的颜色默认为颜色1,现在有T种颜料,两种操作,一种是在块A与块B之间涂上颜色C,另一种是输出块A与块B之间有多少种不同的颜色,共有O项操作。
分析 这一题是一道典型的线段树的应用问题。因为T小于30,可以利用二进制操作,把区间的颜色属性作为线段树结点的标记数据。1表示有这种颜色,0表示没有这种颜色。二进制序列“10000001000010000100000000000000”表示该区间有颜色1、颜色8、颜色13和颜色18这四种颜色。在查询某区间块含有多少种颜色时,将区间的颜色属性二进制序列从左到右扫描,序列中1的个数即为区间的颜色种数。
解
#include <stdio.h>
#define max_n 100000
struct _tNode
{
int l;
int r;
int c;
int lazy;
}node[4 * max_n + 1];
void up(int k)
{
node[k].c = node[k * 2].c | node[k * 2 + 1].c;
}
void down(int k)
{
if (node[k].lazy)
{
node[k * 2].lazy = node[k * 2 + 1].lazy = node[k].lazy;
node[k * 2].c = node[k * 2 + 1].c = node[k].lazy;
node[k].lazy = 0;
}
}
void build(int k, int l, int r)
{
if (l > r) return;
node[k].l = l;
node[k].r = r;
node[k].lazy = 0;
if (l == r)
{
node[k].c = 1;
return;
}
int m = (l + r) / 2;
build(k * 2, l, m);
build(k * 2 + 1, m + 1, r);
up(k);
}
void paint(int k, int l, int r, int c)
{
if (node[k].l >= l && node[k].r <= r)
{
node[k].c = 1 << (c – 1);
node[k].lazy = 1 << (c – 1);
return;
}
down(k);
int m = (node[k].l + node[k].r) / 2;
if (l <= m)
paint(k * 2, l, r, c);
if (r > m)
paint(k * 2 + 1, l, r, c);
up(k);
}
int query(int k, int l, int r)
{
int a = 0, b = 0;
if (node[k].l >= l && node[k].r <= r)
return node[k].c;
down(k);
int m = (node[k].l + node[k].r) / 2;
if (l <= m)
a = query(k * 2, l, r);
if (r > m)
b = query(k * 2 + 1, l, r);
return a | b;
}
int main(void)
{
int n, t, o;
char op;
int l, r, c;
scanf(“%d %d %d”, &n, &t, &o);
build(1, 1, n);
while (o–)
{
scanf(” %c”, &op);
if (op == ‘C’)
{
scanf(“%d %d %d”, &l, &r, &c);
if (l > r)
{
l = l ^ r;
r = l ^ r;
l = l ^ r;
}
paint(1, l, r, c);
}
else if (op == ‘P’)
{
int total;
int sum = 0;
scanf(“%d %d”, &l, &r);
if (l > r)
{
l = l ^ r;
r = l ^ r;
l = l ^ r;
}
total = query(1, l, r);
while (total)
{
if (total & 1)
sum++;
total >>= 1;
}
printf(“%d\n”, sum);
}
}
}
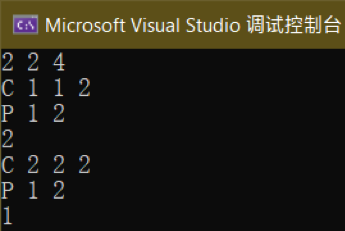
运行结果如图3.1所示。
提交结果如图3.2所示。
4 总结
线段树是一种高级数据结构,利用好线段树,可以高效率地解决区间问题和线段问题。线段树的数据结构还可以使用链式结构,减少空间占用,缺点是结点的访问效率会有所降低。
文中线段树数组长度为4n+1,在实际应用上并用不到那么多,这造成了大量的空间浪费,可以利用深度优先搜索序列进行优化,代替原数组下标,可以把空间占用压缩到2n+1。
5 参考资料
1.Segment tree. https://en.wikipedia.org/wiki/Segment_tree. Wikipedia.
2.★忆先★.《[奇怪但有用的数据结构]线段树》. https://cloud.tencent.com/developer/article/1149069. 腾讯云.
3. TRTTG. 《浅谈线段树》. https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html. 博客园.

0 条评论